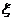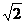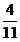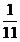2015新余二模理科数学答案
19.解:(1)若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,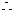 共有8C
共有8C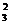 对相交棱。
对相交棱。
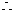 P(
P(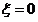 )=
)=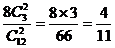 …………………………………4分
…………………………………4分
(2)若两条棱平行,则它们的距离为1或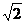 ,其中距离为
,其中距离为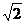 的共有6对,
的共有6对, P
P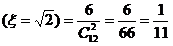 ,
,
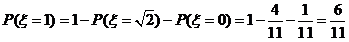
 随机变量
随机变量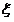 的分布列是:
的分布列是:
|
|
0 |
1 |
|
|
P |
|
|
|
……………………10分
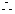 其数学期望
其数学期望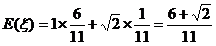 。…………………………12分
。…………………………12分
20.解:(1)由题设知:因为抛物线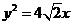 的焦点为
的焦点为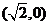 ,
,
所以椭圆中的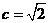 ,又由椭圆的长轴为4,得
,又由椭圆的长轴为4,得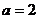 ,
,
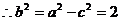
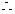 椭圆的标准方程为:
椭圆的标准方程为: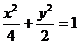 …………4分
…………4分
(2) 法一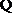 直线
直线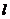 斜率不为零,
斜率不为零,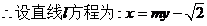 ,代入椭圆方程得:
,代入椭圆方程得: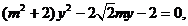
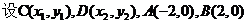
则有: 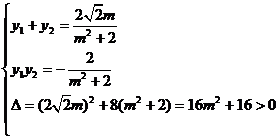 …………5分
…………5分
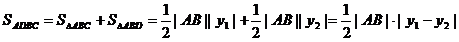
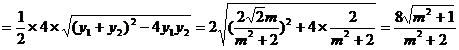
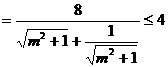
(当且仅当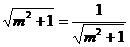 ,即
,即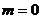 时等号成立)
时等号成立)
四边形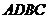 的面积的最大值为4 …………8分
的面积的最大值为4 …………8分
法二:当直线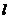 斜率不存在时 ,
斜率不存在时 ,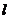 的方程为:
的方程为: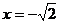 ,此时
,此时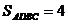 …………5分
…………5分
当直线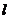 斜率存在时,设
斜率存在时,设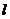 的方程为:
的方程为: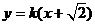 (其中
(其中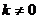 ) 即
) 即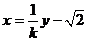 代入椭圆方程得:
代入椭圆方程得: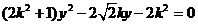 ,
,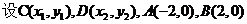
 …………5分
…………5分
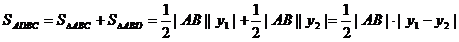
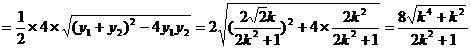
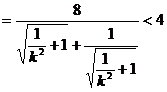
综上所述:四边形 的面积的最大值为4 …………8分
的面积的最大值为4 …………8分
(3)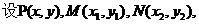 由
由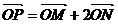 ,可得
,可得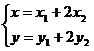 …①
…①
又因为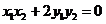 ……②
……②
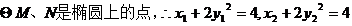
由①②可得: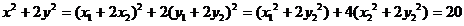
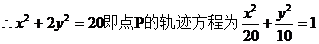 ……11分
……11分
由椭圆的定义存在两定点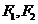 使得
使得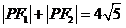 ………12分
………12分
21.解 (1)f′(x)=ex+e-x-2≥0,等号仅当x=0时成立.
所以f(x)在(-∞,+∞)上单调递增.…………………………………1分
(2)g(x)=f(2x)-4bf(x)=e2x-e-2x-4b(ex-e-x)+(8b-4)x,[来源:Z_xx_k.Com]
g′(x)=2[e2x+e-2x-2b(ex+e-x)+(4b-2)]=2(ex+e-x-2)(ex+e-x-2b+2).
①当b≤2时,g′(x)≥0,等号仅当x=0时成立,所g(x)在(-∞,+∞)上单调递增.
而g(0)=0,所以对任意x>0,g(x)>0;……………………………3分
②当b>2时,若x满足2<ex+e-x<2b-2,即0<x<ln(b-1+)时g′(x)<0.
而g(0)=0,因此当0<x≤ln(b-1+)时,g(x)<0…………………6分
综上 ,b的最大值为2……………………………7分
,b的最大值为2……………………………7分
(3)由(2)知,g(ln)=2-2b+2(2b-1)ln2.
当b=2时,g(ln)=2-4+6ln2>0,ln2>12>0.692 8;………………8分
当b=4+1时,ln(b-1+)=ln,
g(ln)=-2-2+(3+2)ln2<0,
ln2<28<0.693 4…………………………………………11分
所以ln2的近似值为0.693………………………………12分
22解:(1)连结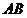 ,
,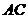 ,由题设知
,由题设知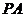 =
=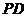 ,故∠
,故∠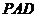 =∠
=∠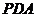 .
.
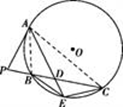 因为∠
因为∠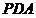 =∠
=∠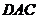 +∠
+∠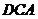
∠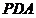 =∠
=∠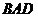 +∠
+∠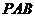
∠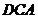 =∠
=∠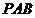 ,
,
所以∠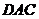 =∠
=∠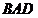 ,从而.
,从而.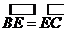 因此
因此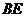 =
=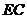 ……………………………5分
……………………………5分
(2)由切割线定理得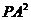 =
=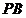 ·
·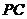 . 因为
. 因为 =
=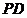 =
=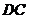 ,所以
,所以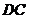 =
=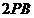 ,
,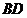 =
=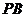 ,
,
由相交弦定理得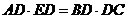
所以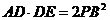 …………………………10分
…………………………10分
解23.(1)由曲线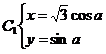 。得
。得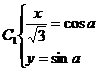
两式两边平方相加得: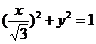
即曲线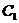 的普通方程为:
的普通方程为: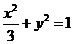
由曲线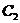 :
: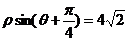 得:
得: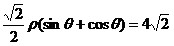
即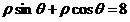 ,所以
,所以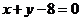
即曲线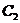 的直角坐标方程为:
的直角坐标方程为: 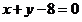 ……………………………5分
……………………………5分
(2) 由(1)知椭圆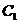 与直线
与直线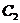 无公共点,椭圆上的点
无公共点,椭圆上的点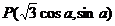 到直线
到直线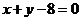 的距离为
的距离为
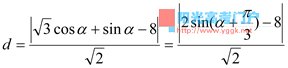
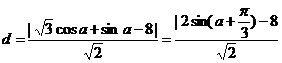
所以当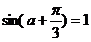 时,
时,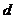 的最小值为
的最小值为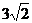 ,此时点
,此时点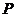 的坐标为
的坐标为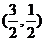 ………10分
………10分
24.解:(1)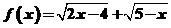
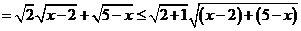 =3,
=3,
当且仅当x=4时等号成立.
故函数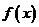 的最大值M=3…………………………………5分
的最大值M=3…………………………………5分
(2)由绝对值三角不等式可得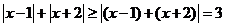 .
.
所以不等式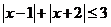 的解x就是方程
的解x就是方程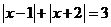 的解.
的解.
由绝对值的几何意义得,当且仅当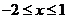 时,
时,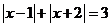 .
.
所以不等式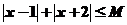 的解集为
的解集为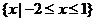 ……………………10分
……………………10分